Cantor’s Diagonal Proof
Cantor’s diagonal argument is a proof devised by Georg Cantor to demonstrate that the real numbers are not countably infinite. Suppose that all real numbers in the section from 0 to 1 are shown by infinite binary fractions, and they are put into one-to-one correspondence with all natural numbers. We could then enumerate all real numbers in this interval as a sequence, R
1,R
2,R
3, … :

In this sequence, anm is the m-th digit of the Rn and diagonal digits are enclosed in square brackets. Consider an infinite binary fraction X =0.b1b2…bn… . We can compose the new number X as follows: if a11 of R1 is 0 then b1 is 1, if a22 of R2 is 1 then b2 is 0, and so on. Finally, we can get the new number X: X differs in the n-th binary place from Rn. So this new number X is not in our sequence. In conclusion, the assumption, that all real numbers in the interval [0,1] are put into one-to-one correspondence with all natural numbers, must be false. Then, all real numbers between 0 and 1 is strictly larger than all natural numbers. Q.E.D.
The Counterargument Against Diagonal Procedure
Cantor’s diagonal argument uses the completion of infinite processes. However, the mathematicians before Cantor did not accept the completion of infinite processes. This is the controversial point of Cantor’s diagonal argument. To avoid this point, we shall discuss within the range of finite binary fractions. In addition, we shall write numbers in binary notation in equations. First, we enumerate all 11-digit binary fractions in the interval [0,1] in ascending order:
In this sequence, F11(m) is the m-th 11-digit binary fraction and diagonal digits are enclosed in square brackets. Using Cantor’s diagonal procedure, we can compose the number X = 0.111, which differs from the diagonal number in each digit. However, X is different from only the first three numbers in this sequence and then X equals to F11(1000).
Next, we enumerate all n-bit binary fractions in the interval [0,1] in ascending order:
In this sequence, Fn(m) is the m-th n-bit binary fraction and diagonal digits are enclosed in square brackets. We compose the number X in the above mentioned manner. However X differs from only first n numbers in this sequence. This sequence contains X because it includes all n-bit binary fractions in the interval [0,1].
Next, the diagonal number is only n-bits after the binary point. On the contrary, this sequence contains 10n+1 binary fractions. The ratio n/(10n+1) is monotonically decreasing. As n increases, n/(10n+ 1) approaches 0:

Therefore, Cantor’s diagonal argument has no application to all n-bit binary fractions in the interval [0,1].
Approximation of Real Numbers
Consider a real number α in the interval [0,1]. If α is not a binary fraction, then α lies between two n-bit binary fractions and there exists a natural number m:
We can approximate the real number α by Fn(m) and then the error is less than 1/10n:
As n increases, then Fn(m) approaches α:
At the time, the number of all n-bit binary fractions in the interval [0,1] is consistently 10n+1. No matter how large n is, 10n+1 is a natural number. In conclusion, all n-bit binary fractions in the interval [0,1] are constantly countable.
Where Is Cantor’s Paradise?
We shall use decimal notation in last two sections. Consider the sequence of all 150-digit binary fractions in the interval [0,1]. Our sequence consists of approximately

binary fractions. Let us compare this number with the diameter of the observable universe. We choose the diameter of a proton as the reference length for measuring the diameter of the observable universe. The ratio of
the diameter of the observable universe to
the diameter of a proton is roughly

. Even if we could use proton sized digits, we could not write our sequence in one column in our observable universe. At the time, the diagonal number differs from only 150 binary fractions of our sequence. This means that Cantor’s diagonal argument cannot apply
in our observable universe. Where is Cantor’s paradise?
The Pigeonhole Principle
Next, we shall compare the number of irrational numbers with that of binary fractions in the interval [0,1]. Let us regard an irrational number as a pigeon and an interval of adjacent two n-bit binary fractions as a pigeonhole. According to the
pigeonhole principle, if the number of irrational numbers were larger than that of binary fractions, there would be at least two irrational numbers, between which there is no binary fraction. However, there is not such a pair of irrational numbers. The proof is as follows. Consider arbitrary two irrational numbers α and β in the interval [0,1]. If the difference of them is zero, they are the same number. If they are different numbers, the difference isn’t zero. Let us assume that the difference is ε:

There exists a natural number n such that:
For enough large n, there are two natural numbers l and m such that:
So, we can sandwich any two irrational numbers by different pairs of n-bit binary fractions. According to the pigeonhole principle, the number of irrational numbers is not larger than that of binary fractions in the interval [0,1]. Evidently, they are countable. Therefore, irrational numbers in the interval [0,1] are countable.
However, there are infinite irrational numbers between two adjacent n-bit binary fractions. We shall consider this problem from the standpoint of the potential infinity. If Aristotle lived now, he would say “There aren’t infinite irrational numbers but there is the possibility of the existence of irrational numbers”. Let us consider the number line. An irrational number corresponds to a point on the number line. Because the point has no magnitude, anyone cannot detect it. That is, it isn’t actually exist. If we want to actualize it, we must locate it on the number line. Hence, it is actualized when it is sandwiched between two adjacent n-bit binary fractions. Needless to say, actualized irrational numbers are countable.









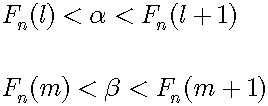
So what? — So … what else is new?Of course the diagonalization argument doesn’t prove that fixed-precision binary fractions of any given length “n” are uncountable — the are not only countable, but finite in number! Not very surprising, is it?
The diagonal procedure can not apply to any n-digit binary fractions and the diagonal number can differ from only n binary fractions. These are evident. But most important point is that the ratio of n to the number of all n-digit binary fractions in interval [0,1], n/(2^n+1), is monotone decreasing. As n increases, effectiveness of diagonal procedure decreases rapidly. Then, infinity is larger than any “n”. Can you apply the diagonal procedure to infinite binary fractions?
Cantors Earlier proof — The Earlier Theorem and Proof Theorem: The real numbers are uncountable. Cantor’s earlier proof (EP) assumes that r_1,r_2,….is a list of reals all in the interval [0..1]. He then constructs, by a limiting process, a real number x that is in the interval [0..1] and satisfies, for all k, x not r_k. This of course shows that the reals are uncountable.Let I_0 = [0..1]. We will follow Cantor and construct a series of proper intervals I_0 contains I_1 contains I_2 …..Suppose that we have constructed I_{k-1} for k geq 1, then we will construct the next interval as follows. Let I_{k-1} = [a..b], Select c so that a < c < band c is not equal to r_k. Then, r_k is in at most one of the two intervals: [a..c] or [c..b].Let I_k be the first interval that does not contain r_k. We claim that the nested intervals I_k tend to an interval I_inf, which can be degenerate. Let x be any point in I_inf. By construction, x is in [0..1]. Moreover, x cannot be equal to any r_k. This follows since at step k we selected I_k so that r_k not in I_k. But, since I_inf is in I_k, it follows that r_k is not in I_infNote, the fact that nested closed intervals tend to a limit interval is the place where Cantor uses the fact that the reals are complete. That is any bounded increasing (decreasing) sequence of reals has a limit point.diagonal method over and over, could it be possible that the EP method could have some advantage in solving some problems? http://rjlipton.wordpress.com/2009/04/18/cantors-non-diagonal-proof/
Absolutely… incorrect — Kotani, First, your list has 9 numbers not 11. Your equation appears extremely wrong, perhaps 2^n+1? Anyway, the rest of your mathematical errors will be addressed below. However, your last paragraph claims if it cannot be seen or written it cannot exist! I cannot see air, I have never seen China, I have never seen dark matter, etc, these things exist do they not?You believe the reals countable because you believe an infinite string of 0,1’s are countable.However, your induction is wrong. Your assumption requires there exists a bijective function from n to P(n). This however is not true. In the example you constructed you showed Cantor’s diagnolization is incorrect for n=3. In your argument you missed the crux. In order to prove a bijection you show the Codomain equals the range of f. From this, you can see you actually show that given a n, I cannot created a bijection to P(n). This induction shows P(n) is uncountable given the logic you used. Hence, do you understand the key point missing, you believe that because both range and codomain are finite in your example the codomain is countable. However, when extending your idea to w, you are right |V| > |H|, this is why V is uncountable.
Please read first paragraph of second section of this knol.This sentence: In addition, we shall write numbers in binary notation in equations.However,to avoid misunderstanding, I added as follows: We shall use binary number system in this knol except last section.I use binary number system in this knol.My list has 9 numbers and 9 is converted to 1001 in base 2.Obviously, Cantor’s diagonal argument can not apply to all n-digit binary fractions in interval [0,1].Because the observable universe is finite, Cantor’s diagonal argument is incorrect in our universe.If we could use digits as small as we want, we cold not apply Cantor’s diagonal argument to our list in our universe.
So the belief is only finite things exist. Then under this concept what is 1/3? This has no finite representation.I iterate again, all you have shown is that there are vastly more vertical things than horizontal length. So no bijection could possibly exist. In your “proof” you have {f(1),f(2),…,f(9)} for n = 3. However, how can you have f(4), 4 is not defined since you are restricted to 3 things. You confused finiteness of your case implies Cantors logic is wrong.However, consider the following thought experiment:The observable universe is “finite” and expanding, but It could also be non-finite at the same time. Consider the possibility that the observable universe is closed, i.e. movement, light. Hence, it could be imagined as a giant ball, taurus, yes? Given light has a fixed speed and information associated with it, if large enough the observable universe would be able to observe itself at an earlier state. If the premises are true then there is an infinite loop.Interesting question arrises:So if I were to take universes which observe this universe as the notion past, will I have enough length than?”finite” is like “finite” like the byte representation on a CD, which I believe was on the order of 2^(10^(6000000))), not sure about it, but a huge number which has a bijective correspondence to any possible sound made in this universe.
1/3 is ratio of 1 to 3.This is finite representation.Then, we shall consider decimal representation of 1/3 in real world.Pure mathematics can not directly apply to real world but practical science can apply.Because we must consider error in practical science, significant figures are important.If decimal representation of 1/3 is 0.33, there are 2 significant figures.Below is the list of all 4-digit binary fractions in interval[0,1].0.00000.00010.00100.00110.01000.01010.01100.01110.10000.10010.10100.10110.11000.11010.11100.11111.0000Above list has 17 numbers but the diagonal number can cover only 4 numbers.Therefore, diagonal argument can not apply to above list.Next thought experiment is very interesting.
Kotani-sama,Here is what I am saying, you have length n=4. So let us Consider f(1), f(2), f(3), f(4)…WLOG f(1) = .1010, f(2) =.1011, f(3)= .0001, f(4) = .1100. Understand? Now I will show given this map f to the interval [0..1]_2 to 4 decimal places is not bijective. Using Cantor’s diagonalization I get x =.0111. Which f(n) maps to it? clearly not f(1), f(2), f(3), f(4). You cannot use f(5) since you have already exhausted your contraint of 4 things. Do you understand?If the Reals were countable than, there would be as many reals as digits because the digits are countable.For the same reason you cannot write out 1/3, yet it exists is the same for Cantor’s argument.
That is the point, if the length of digit strings is countable, then you can only have countably many this to pair in the list.My example shows that if the length is 4, you can only use 4 things! You cannot say I limit the string to 4 but I can map any number I want, you are restricted to 4 elements, you cannot use more because it is undefined as you have n = 4.
John Smith,Your list is below.0.10100.10110.00010.1100Above is the 4X4 list. Cantor’s diagonalization can esily apply to the list. However, the list contains only 4 numbers of 17 4-digit binary fractions in interval [0,1]. It is no wonder that we got the new number by Cantor’s diagonalization.
All 4-digit binary fractions are well defined.There are 17 4-digit binary fractions in interval [0,1].Why elements of your set are restricted to 4?
Kotani,The length of an infinite string of digits is the cardinality of the natural numbers, omega. Hence, if you want to use a finite example, like 4, you must restrict yourself to only counting that many, as we are restricted to only counting with natural numbers. Now you knol shows for any length string there is no bijection. However, you are stuck on the fact of finite.Yes, there are 17 binary representations of the interval [0..1] when restrict to length of four decimals. However, you have not defined the notion of 5 let alone 17!Do you understand? If you are using mathematical induction you must make sure your premises never change, or else you fall into all horses are the same colour falicy.
I discuss the application of Cantor’s diagonal argument to finite numbers.I don’t touch infinity.Then, my list has no relation to the cardinality.I need not restrict myself.
… — And what if a number doesn’t have n-digit binary representation for any n?
If a number is a real number, it is a Dedekind cut. The Dedekind cut divides all n-digit binary fractions into the larger group and the smaller group. Then, the Dedekind cut has n-digit binary representation.If a number has no n-digit binary representation, the number is not a real number.
Lists are longer than they are wide. — If you list the first 8 binary numbers, or the first 16, you will see that each list is longer than the numbers themselves. Each of the first 8 can be written using 3 digits. Each of the first 16 can be written using 4 digits. In fact, for any such list of finite length strings the list itself is longer than the strings.Diagonalization applied to such lists does not work to produce numbers not already in the list.This relationship holds, apparently, for any such length even as it increases without limit. Why, therefore, should we accept the assumption, present in Cantor’s argument, that it does not hold in the case that the string length is infinite?
An arbitrary natural number is finite.The proof by mathematical induction is below.1. 1 is a finite number.2. If n is a finite number, then n+1 is a finite number.3. An arbitrary natural number is absolutely finite.That is, there is no infinite natual number.No matter how many finite numbers are collected, the total number is finite.So, we cannot reach infnite digits.Therefore, Cantor’s standpoint is God’s one.Human beings cannot know how he jumped to infinity.
There is one more important point.Cantor’s argument contradicts epsilon-delta proof.According to the epsilon-delta proof, width/length of the list converges to zero.When we increase digits of the list, width/length monotonically decreases.So, we can easily accept the result.However, Cantor’s argument is as follows.When the number of digits reaches the actual infinity, suddenly width/length becomes 1.I can’t accept Cantor’s argument.
A long analysis — Hello. I’ve read your proof, and it is not valid. I don’t think the other commenters have precisely identified the error however, so I’ll attempt to do so. To begin with, before I point out what’s wrong with your proof, let me point out what is correct. First of all, it is correct that you cannot apply Cantor’s diagonal argument if you are looking for function from the natural numbers to the set of all numbers between 0 and 1 with finite binary expansions (what I believe you call binary fractions). Those are indeed countable. In fact there is a shorter argument you can use; define the map 1 -> 0.1 10 -> 0.01 11 -> 0.11 100 -> 0.001 101 -> 0.101 110 -> 0.011 111 -> 0.111 1000 -> 0.0001 1001 -> 0.1001 I hope the the pattern is clear; we take each natural number, take it’s binary representation, reverse it, and insert a decimal point to get the binary representation of a real number between 0 and 1. I think it’s evident that every finite binary fraction in the interval (0,1) is in the range of this function. And in fact more is true. The rational numbers are countable, and the finite binary fractions are a subset of the rational numbers, so of course they are countable too. But of course this does not prove the set of all real numbers in (0,1) is uncountable. The third part of your proof is also correct; between every two irrational numbers, there is a finite binary fraction (indeed, there an infinite number of them). This is an example of what is called the Archimedean principle. The error in your proof occurs in the second part, where you assert these two statements are inconsistent. You wrote: “Next, we shall compare the number of irrational numbers with that of binary fractions in the interval [0,1]. Let us regard an irrational number as a pigeon and an interval of adjacent two binary fractions as a pigeonhole. According to the pigeonhole principle, if the number of irrational numbers were larger than that of binary fractions, there would be at least two irrational numbers, between which there is no binary fraction.” Your use of the term adjacent in “an interval of adjacent two binary fractions” makes no sense. There is no such thing as an “adjacent pair” of binary fractions. There do exist adjacent pairs of integers. 5 and 6 are adjacent integers, because there is no integer between them. 11 and 12 are adjacent integers for the same reason. However, 0.10 and 0.11 are not adjacent binary fractions, because the binary fraction 0.101 falls between them. 0.10 and 0.101 are not binary adjacent fractions, because 0.1001 fall between them. And so on. Between any two distinct pair of binary fractions, there exists a binary fraction between them; in fact there exists an infinite number of them. Therefore, there is no such thing as adjacent binary fractions (using the order inherited from the real numbers). Similarly, between any two irrational numbers, there is another irrational number; there is no such thing as adjacent irrational numbers. To put it another way, if you have an integer, it makes sense to ask the question what is the next integer in order after that one? For example, the next biggest integer after 17 is 18. But if you have a binary fraction, it makes no sense to ask what binary fraction is the next in order after that one. What’s the next biggest binary fraction after 0.001100? Not 0.001101, because 0.0011001 is even closer to 0.001100 while being greater than it. And not 0.0011001, because 0.00110000001 is even closer. And so on. Finally, correct me if I’m wrong here, but your argument seems to me to be the following. We argue that the binary fractions must be as numerous as the irrational numbers. First, if the irrational numbers are uncountable, then the set of adjacent pairs of irrational numbers must also be uncountable (as we can map each such pair to it’s left element). And since there is at least one binary fraction falling between each adjacent pair of irrational numbers, and since it’s impossible for the same binary fraction to fall between two different adjacent pair of irrational numbers, there must be at least as many binary fractions as adjacent pairs of irrationals in order to fill them all, and therefore as many binary fractions as irrational numbers. If this is your argument, then the error is that there is no such thing as a pair of adjacent irrational numbers, and there certainly isn’t a set of distinct non-overlapping adjacent intervals that completely cover the interval (0,1), whose endpoints are irrational numbers, and the set of whose endpoints include all the irrational numbers, and that therefore must be filled by distinct binary fractions if there is to be a binary fraction between every pair of irrational values. It seems to me that the mistake you’ve made is taking your intuition of the integers and applying it inappropriately to the rational numbers and to the real numbers. If we have five numbers strung out on a line one after the other r1 r2 r3 r4 r5 and if I want to…
I’m so sorry, I typed in this comment with proper formatting, but when I hit submit, it turned into an unreadable wall of text. I will send you an email instead.
I’m sorry for this late reply. Your comment is very interesting, and I want to read all sentences of your comment. Please send me email. kotanikazuhiko@gmail.com
You correctly pointed out my mistake. So, “an interval of adjacent two binary fractions” is nonsense. However, I wanted to say “an interval of adjacent two n-bit binary fractions”. I missed n-bit. Now, I have corrected the mistake. Thank you.