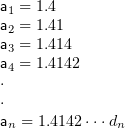The Actually Infinite Decimal Is Not a Decimal

I shall consider the potentially infinite decimal based on the potential infinity. An irrational number is approximated by the n-digits decimal. Then, we can make the series of approximated values. Consider the potentially infinite decimal representation of  the square root 2. It is represented  by the next series.

The number of digits of a_n is constantly finite. The proof by the mathematical induction is below.

1. Because a₁ has only one digit, a₁ has a finite digit.
2. When a_n has n digits, then a_n+1 has n+1 digits. If n is a finite number, then n+1 is a finite number. Hence, a_n+1 has finite digits.
3. Therefore, a_n has constantly finite decimals.

Furthermore, as mentioned in The Infinite Loop, any natural number is finite. If the number of digits of a decimal is a natural number, it is a finite decimal.

Next, let us consider the actually infinite decimal. Because we cannot attain to infinite digits, we cannot touch it. No matter how many finite numbers we collect, we cannot reach it. However, any finite part of it is identical to the corresponding potentially infinite decimal. That is, arbitrary digit of it equals the corresponding digit of the potentially infinite decimal. The difference between the actually infinite decimal and the potentially infinite decimal is only whether there are infinite digits or not. That is, the actual infinite decimal can be substituted for the potentially infinite decimal within potentially infinite range..

Finally, the actual infinity must be larger than any natural number. That is, the actual infinity is not a number. The actual infinite decimal is not a decimal. Therefore, the actually infinite decimal is the irrational number itself. In order to avoid confusion, it should be eliminated.